Absolute Value Definition
For any real number, the absolute value or modulus of a number is denoted by , with a vertical bar on each side of the quantity, and is defined as
The absolute value of is thus always either a positive number or zero, but never negative. When is positive or , the absolute value is the number itself. When is negative, the absolute value is negative of that , so the result is ultimately positive.
For example,
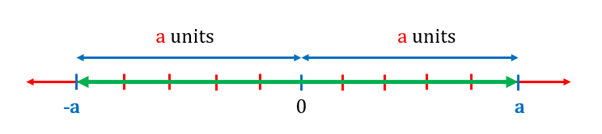
Absolute Value as a Distance from a Point
The absolute value of a real number is that number's distance from zero along the real number line. The absolute value of the difference between two real numbers is their distance. As the distance can never be negative, the absolute value can also never be negative.This can be pictorially represented as follows:
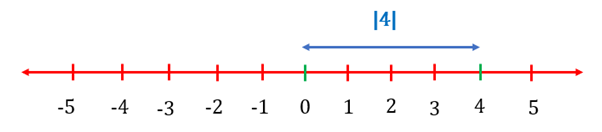
The absolute value of is the distance of from .
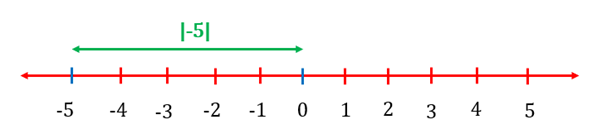
The absolute value of is the distance of from .
Points Representing
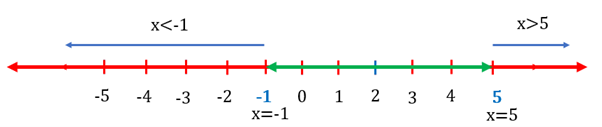
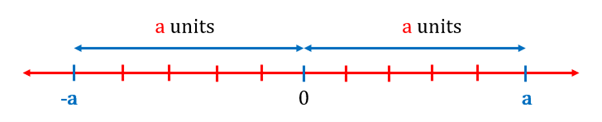
Since is equal to the distance of from the origin, we are looking for those numbers that are lying at a units of distance from zero. We can see from the figure given below that the distance of both the points and is a units from . Hence, the equation represents the points and .
For example, represents the points and and can be represented as
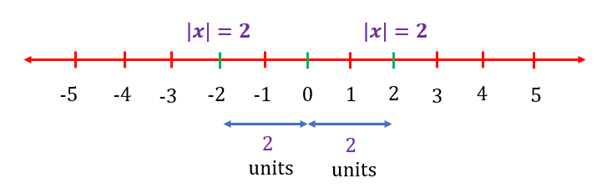
Points Representing
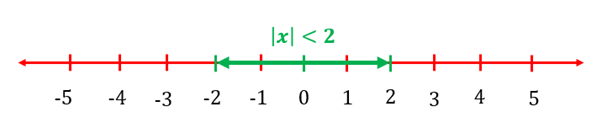
represents the distance of point or from . Hence, represents all the points whose distance from is less than units. All these points can be represented as below:
The thick green region represents the points belonging to . Hence, the points representing the inequation can be defined by the inequality .
For example, can be written as and can be represented as
Absolute Value to Find Distance Between Two Numbers
represents the distance of point from point a. Similarly, represents the distance of the number from the number as . So, when we write the equation , it denotes that the distance between and is units. That is, we are looking for points whose distance from is units. This can be represented as
For example, means the point and that is units away from . We can represent this as
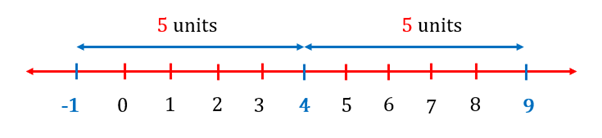
means or .
Region Representing
gives two points for that satisfies the equation. Whereas the inequality represents a region of points for which is less than . In this region, the distance of the point from will be less than . This can be represented as
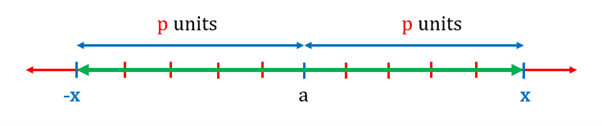
The thick green line represents the points of that satisfy the inequality .
For example, can be represented as below.
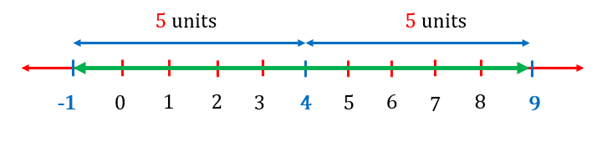
The region can be represented by an open bracket as the endpoints are not valid for the inequality.
Now, what about ? This will be the region outside the boundary of , and it can be shown as
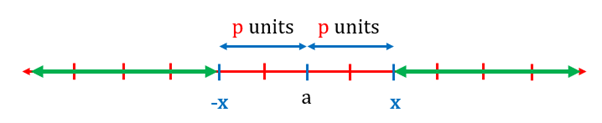
The region shown in a thick green line represents the values satisfying the inequality . The rest of the region of represents .
For example,

is represented by the green region, and is represented by red.
and are the distances of numbers and from . When is lying between and , the sum of the distances of from and is constant and is equal to the distance between and , i.e., . When lies on either side of and , the sum starts increasing as starts moving further away.
Case 1: is lying between and 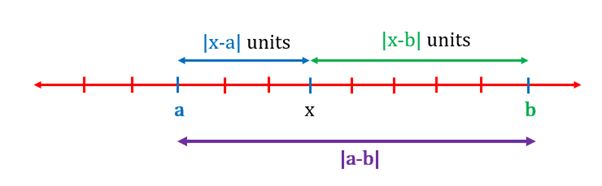
Case 2: lies on either side of and 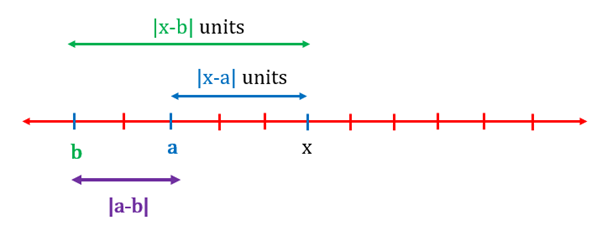
For example, 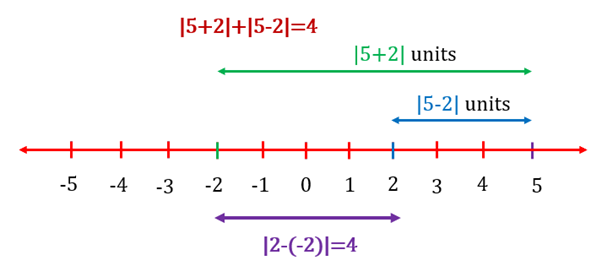
Solved Examples
Q1. Find the value of for which .
Ans: give two points for that satisfy the equation. We need to find the value of such that it is units away from . 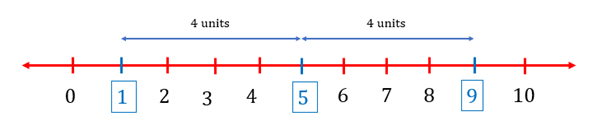
So, and .
Q2. Find the value of for which .
Ans: is the sum of distances of the number from and , respectively. Here, can have two cases,
Case 1: is between and
If lies between and , then . As there are only points between and , between them is impossible.
Case 2: lie on either side of and at a distance and from two numbers as shown below: 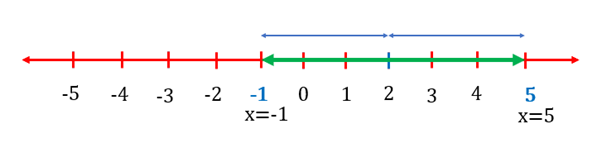
null
Hence, the value of are
Q3. Find the range where .
Ans: Let us first identify the range where . This can be denoted as . 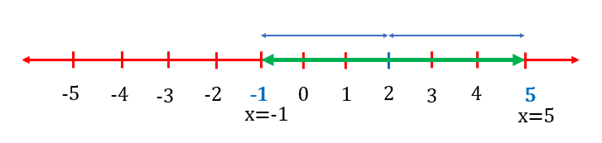
All the values outside this range will satisfy the inequality . It can be denoted as and and represented as