Chicken Nuggets Theorem

Chicken Nugget Theorem: The Chicken nugget theorem states that for any two relatively prime integers $x$ and $y$, the largest integer that cannot be expressed in the form $ax + by$ for non-negative integers $a$ and $b$ is $xy-x-y$.

There is an interesting story behind the chicken nugget theorem. Initially, in the United Kingdom, McDonald's sold their nuggets in packs of $9$ and $20$. So, if you want $12$ McNuggets, you can buy two packs of $6$. On the other hand, you can't buy $11$ nuggets at a time as the only options available are $9$ and $20$. It's impossible. A curiosity was developed among math enthusiasts, and they wanted to answer this question: What is the largest number of McNuggets that you can't buy with packs of $9$ and $20$? After putting in lots of effort, the mathematicians found that the answer is $151$ nuggets. We cannot buy $151$ nuggets with packs of $9$ and $20$, but we can buy any amount larger than $151$. This led to the formation of the Chicken McNugget theorem.

The Chicken McNugget theorem states that for any two relatively prime positive integers $m,n$, the greatest integer that cannot be expressed in the form $am+bn$ for non-negative integers $a, b$ is

In other words, you can't combine packs of $m-$sized and $n-$sized McNuggets to purchase $(mn-m-n)$ McNuggets, but you can buy any amount of McNuggets larger than $(mn-m-n)$. If there exist non-negative integers $a,b$ so that $am+bn=d$, we will say that $d$ is purchasable. If they don't exist, we will say $d$ is unpurchaseable.

A question can arise here, why do $m$ and $n$ have to be relatively prime? Relatively prime integers are those integers which do not have any other common factor than 1. If m and n are not prime, there would be an infinite number of unpurchaseable amounts of McNuggets. As a simple example, if the chicken McNuggets are sold in sizes of 4 and 6, the numbers 4 and 6 are not coprime, as the greatest common factor between them is 2. We can instantly notice that we can't buy any odd number of McNuggets with packs of 4 and 6; hence there is no largest unpurchaseable amount. The Chicken McNugget Theorem is only interesting and valid if m and n are coprime.

Let us visualise this problem. McDonald's is selling the McNuggets in packs of 9 and 20, as given below.

Let us see the number of nuggets we can purchase using this combination.

We can show the possible and impossible combinations in the table given below:

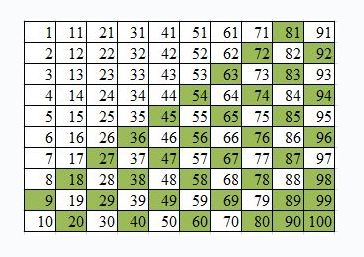
Here, the boxes shaded green show the numbers of Chicken McNuggets that can be purchased with the combo of 9 and 20, and the white boxes show numbers of Chicken McNuggets that cannot be bought.

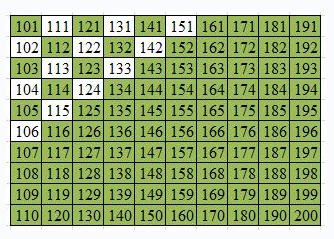
We can see that as the numbers increase, it is more likely to purchase that number of Chicken McNuggets exactly. Only one number from 1 to 10 is purchasable, but six of the numbers from 91 to 100 are purchasable. If we continue the table for another 100 numbers, we find an interesting fact that we can buy all numbers of Chicken McNuggets from 152 to 200.

A consequence of the theorem states that the number of positive integers, which cannot be expressed in the form am+bn is exactly

Even though the theorem is explained using the example of McNuggets, this problem comes up in many real-world contexts.

For example, if we have two tapes that can measure 5 m and 11 m. Then the largest length that cannot be measured using these two tapes will be mn-m-n=5×11-5-11=39 m

Chicken nugget theorem states that for any two relatively prime positive integers m and n, the number d=mn-m-n cannot be expressed as am+bn for any non-negative integers a and b. Any integer n>d can be represented as am+bn for some non-negative integers a and b.

Ans: We know that we can't combine packs of m-sized and n-sized McNuggets to purchase (mn-m-n) McNuggets, but you can buy any amount of McNuggets larger than (mn-m-n). So, the largest number of Mcnuggets that cannot be purchased will be d=(mn-m-n).

Here, m=5 and n=7

Hence, the largest number of Mcnuggets that cannot be purchased =5×7-5-7=35-5-7=30-7=23

Q2. In a restaurant, you can order buckets of doughnuts only in quantities of 7 and 19 a bucket. What is the second largest number of doughnuts you cannot buy?
Ans: We know that we can't combine packs of m-sized and n-sized McNuggets to purchase (mn-m-n) McNuggets. So, the largest number of Mcnuggets that cannot be purchased will be d=(mn-m-n).

Here, m=7 and n=19

Hence, the largest number of Mcnuggets that cannot be purchased =7×19-7-19=133-7-19=107

The second largest number of Mcnuggets that cannot be purchased will be 107-7=100

Q3.How many positive integers cannot be expressed in the form 24a + 7b where a and b are non-negative integers?
Ans: There are exactly (m-1)(n-1)/2 positive integers that cannot be expressed in the form am+bn.

Here, m=24 and n=7

Hence, the number of positive integers that cannot be expressed in form 24a + 7b =(24-1)(7-1)/2=(23×6)/2 =69