Descartes's Rule of Signs: Descartes's rule of signs is a rule for finding the maximum number of positive real roots of a polynomial equation in one variable. It is decided based on the number of times the signs of its non-zero real number coefficients change when the polynomial terms are arranged in descending order of powers, from highest power to lowest power.
Introduction to Descartes's Rule of Signs
A polynomial is an algebraic expression with one or more terms with exponents or powers of the variable as whole numbers. For example, x, x+1, x3+x2+x+1, x100-10,…. The degree of a polynomial is the largest power of the variable in a term in the polynomial expression. The zeros or roots of a polynomial are the values of the variable for which the polynomial equals zero. For a polynomial with degree n, there will be at most n roots. Descartes's rule of signs was first described by René Descartes. It is a method for determining the number of positive real roots of a polynomial. The rule states that for a polynomial in standard form, the number of positive real roots is either at most the number of sign changes in the sequence of the polynomial coefficients, eliminating the zero coefficients or down by an even number.
Definition of Descartes's Rule of Signs
If f(x) a polynomial in one variable such that
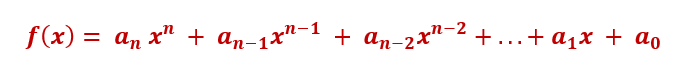
with terms arranged in the descending order of the powers of the variable eliminating the zero coefficients, then by Descartes's rule of signs
* The number of positive real roots or zeros of f(x) is either equal to the number of sign changes of the coefficients in f(x) or less than the number of sign changes by an even number.
* The number of negative real roots or zeros of f(x) is either equal to the number of sign changes of the coefficients in f(-x) or less than the number of sign changes by an even number.
Descartes's Rule of Signs to Find the Number of Positive Real Roots
Let us understand the rule by an example. Let f(x)=ax6-bx5+cx4-dx3+ex2+gx+h
Here, we can see that the terms are arranged in the descending order of powers, and there are no zero coefficient terms. Consider the signs of the coefficients.
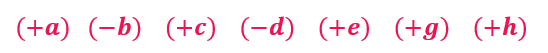
Introduction to Descartes's Rule of Signs
A polynomial is an algebraic expression with one or more terms with exponents or powers of the variable as whole numbers. For example, x, x+1, x3+x2+x+1, x100-10,…. The degree of a polynomial is the largest power of the variable in a term in the polynomial expression. The zeros or roots of a polynomial are the values of the variable for which the polynomial equals zero. For a polynomial with degree n, there will be at most n roots. Descartes's rule of signs was first described by René Descartes. It is a method for determining the number of positive real roots of a polynomial. The rule states that for a polynomial in standard form, the number of positive real roots is either at most the number of sign changes in the sequence of the polynomial coefficients, eliminating the zero coefficients or down by an even number.
Definition of Descartes's Rule of Signs
If f(x) a polynomial in one variable such that
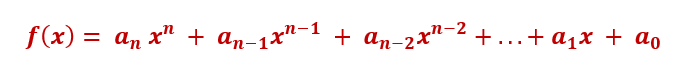
with terms arranged in the descending order of the powers of the variable eliminating the zero coefficients, then by Descartes's rule of signs
* The number of positive real roots or zeros of f(x) is either equal to the number of sign changes of the coefficients in f(x) or less than the number of sign changes by an even number.
* The number of negative real roots or zeros of f(x) is either equal to the number of sign changes of the coefficients in f(-x) or less than the number of sign changes by an even number.
Descartes's Rule of Signs to Find the Number of Positive Real Roots
Let us understand the rule by an example. Let f(x)=ax6-bx5+cx4-dx3+ex2+gx+h
Here, we can see that the terms are arranged in the descending order of powers, and there are no zero coefficient terms. Consider the signs of the coefficients.
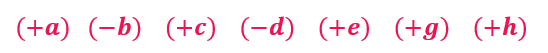
We can see that the signs are changing between some of the terms. Mark and count them.

The signs of the coefficients are changed four times in this polynomial expression. Hence, the number of positive real roots will be at most 4 for this polynomial. The number of roots need not be exactly 4; it can be down by an even number. The number of real roots can be either 4, or 4-2=2 roots or 4-4=0 roots. We can also state this as a polynomial function f(x) arranged in descending order of powers without any zero coefficient terms cannot have more positive real roots than the number of sign changes in it.
Descartes's Rule of Signs to Find the Number of Negative Real Roots
Now, let us find the number of negative real roots. For that, we need to find f(-x). f(-x) is obtained by substituting x with (-x) in the polynomial expression.
⇒f(-x)=a(-x)6-b(-x)5+c(-x)4-d(-x)3+e(-x)2+g(-x)+h
⇒f(-x)=ax6+bx5+cx4+dx3+ex2-gx+h
Now, consider the signs of the coefficients.

The signs of the coefficients are changed four times in this polynomial expression. Hence, the number of positive real roots will be at most 4 for this polynomial. The number of roots need not be exactly 4; it can be down by an even number. The number of real roots can be either 4, or 4-2=2 roots or 4-4=0 roots. We can also state this as a polynomial function f(x) arranged in descending order of powers without any zero coefficient terms cannot have more positive real roots than the number of sign changes in it.
Descartes's Rule of Signs to Find the Number of Negative Real Roots
Now, let us find the number of negative real roots. For that, we need to find f(-x). f(-x) is obtained by substituting x with (-x) in the polynomial expression.
⇒f(-x)=a(-x)6-b(-x)5+c(-x)4-d(-x)3+e(-x)2+g(-x)+h
⇒f(-x)=ax6+bx5+cx4+dx3+ex2-gx+h
Now, consider the signs of the coefficients.
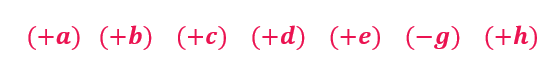
We can see that the signs are changing between some of the terms. Mark and count them.
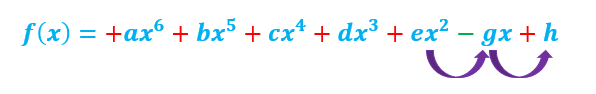
The signs of the coefficients are changed two times in this polynomial expression, and hence the number of negative real roots will be at most 2 for this polynomial. The number of roots need not be exactly 2; it can be down by an even number. That is, the number of negative real roots can be either 2 or 2-2=0 roots. We can state this also as, for a polynomial function f(x) in standard form, the number of negative real roots cannot be more than the number of sign changes in f(-x). If the number of sign changes is zero or one, there is exactly zero or one positive or negative root, respectively, as an even number cannot reduce it. Descartes's rule of signs will not find where the polynomial zeroes are, but the rule will help discover how many roots can be expected and of which type. Descartes's Rule of Signs Chart Descartes' rule of signs gives the possible number of positive and negative real roots, but it cannot provide the exact number of roots. There can be a different combination of the number of roots. So, we can construct a chart with all these possibilities of the number of positive or negative real roots and imaginary roots. While constructing the chart, keep in mind the following: The number of roots or zeros of a polynomial function equals the degree of the polynomial, considering the roots with multiplicities as independent roots.

The number of positive or negative real roots or zeros is either equal to the number of sign changes of f(x) or f(-x) or less than the number of sign changes by an even number.
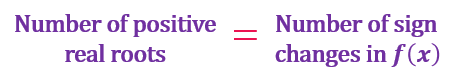
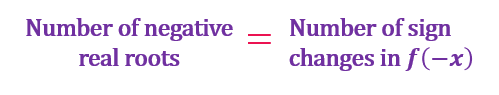
If the number of positive or negative real roots is 0 or 1, then the actual number of roots will be that itself, as an even number cannot further reduce it. Hence, 0 or 1 in any chart column is not to be altered throughout the chart. The roots that are not real are imaginary or complex, and the imaginary roots always occur in pairs. For example, if 1+ i is a root, then 1-i is also a root. The number of complex roots can be obtained by subtracting the sum of positive and real roots from the degree of the polynomial.
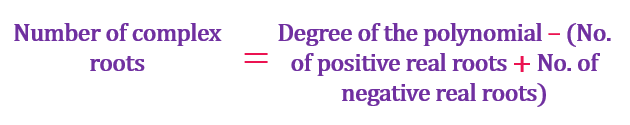
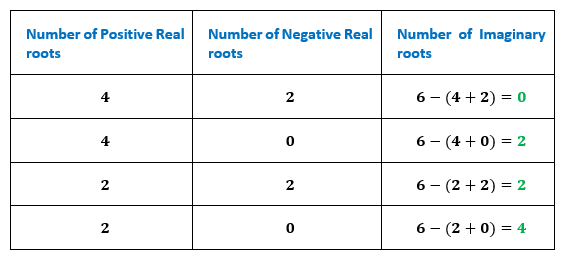
Considering the same example, f(x)=ax6-bx5+cx4-dx3+ex2+gx+h
Here, the possible number of positive real roots is 4,2,0, and the possible number of negative real roots is 2,0. Hence, Descartes's rule of signs chart can be constructed as follows:
Conclusion
Descartes's rule of signs states that for any polynomial f(x) in standard form, without any zero coefficient terms, the number of positive real roots will be either equal to the number of sign changes of the coefficients or down by an even number. The number of negative real roots is either equal to the number of sign changes of the coefficients of f(-x) or down by an even number. The rule will not give the actual number of roots but the possible number of roots. If the number of sign changes of f(x) or f(-x) is 0 or 1, then that itself is the actual number of real roots as it cannot be decreased further by an even number anymore. The number of complex roots can be found using Descartes's sign rule chart.
Solved Examples
Q1. Find the number of positive real roots for the polynomial 3x2–x–12–x4+x3.
Ans: Here, f(x)= 3x2–x–12–x4+x3
f(x) is not in standard form. The standard form of a polynomial is expressed by arranging the terms in the descending order of powers of the variables. So, f(x) in standard form is
f(x)= –x4+x3+3x2–x–12
Now, observe the sign changes in f(x).
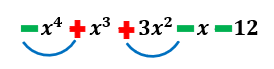
We can see that there are two sign changes; hence, the number of positive real roots can be either 2 or down by an even number, 2-2=0. It has 2 sign changes. Hence, 2 or 0 positive roots.
Q2. Find the possible number of real roots of the polynomial 2x3-x2-15 x+24.
Ans: Given polynomial is f(x)=2x3-x2-15x+24
We can see that there are two sign changes in the coefficients of f(x).
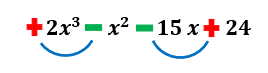
The number of possible positive real roots will be either equal to the number of sign changes or down by an even number. Hence, the possible positive roots are 2 or 0. Now, to find the possible number of negative real roots, let us first find out f(-x).
f(-x)=2(-x)3-(-x)2-15(-x)+24
⇒f(-x)=-2x3-x2+15x+24
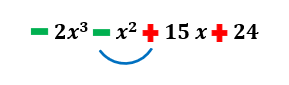
f(-x) has only 1 sign change. Hence, the possible number of negative roots will be 1.
Hence, 2x2-x2-15x+24 can have 2 positive real roots and 1 negative real root.
Q3. Find the possible number of combination of real and imaginary roots for the polynomial f(x) =x5 –3x3+6x2–28x+24.
Ans: Here, f(x) =x5 –3x3+6x2–28x+24
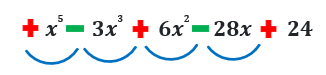
We can see that there are 4 sign changes. So, the possible number of positive real roots will be 4 or 4-2=2 or 2-2=0. The number of negative real roots is either at most the number of sign changes in the sequence of the polynomial coefficients of f(-x), eliminating the zero coefficients or down by an even number.
f(-x) =(-x)5 –3(-x)x3+6(-x)x2–28(-x)+24
⇒f(-x)=-x5 +3x3+6x2+28x+24
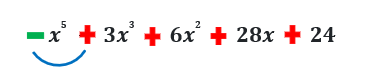
There is only 1 sign change in f(-x). Hence, the possible number of negative roots is one.
Since the degree of the given polynomial is 5, there will be 5 roots for f(x). The number of complex roots is obtained by subtracting the sum of positive and real roots from the degree of the polynomial.
So, Descartes's sign rule chart can be constructed as given below:

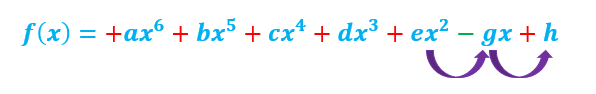
The signs of the coefficients are changed two times in this polynomial expression, and hence the number of negative real roots will be at most 2 for this polynomial. The number of roots need not be exactly 2; it can be down by an even number. That is, the number of negative real roots can be either 2 or 2-2=0 roots. We can state this also as, for a polynomial function f(x) in standard form, the number of negative real roots cannot be more than the number of sign changes in f(-x). If the number of sign changes is zero or one, there is exactly zero or one positive or negative root, respectively, as an even number cannot reduce it. Descartes's rule of signs will not find where the polynomial zeroes are, but the rule will help discover how many roots can be expected and of which type. Descartes's Rule of Signs Chart Descartes' rule of signs gives the possible number of positive and negative real roots, but it cannot provide the exact number of roots. There can be a different combination of the number of roots. So, we can construct a chart with all these possibilities of the number of positive or negative real roots and imaginary roots. While constructing the chart, keep in mind the following: The number of roots or zeros of a polynomial function equals the degree of the polynomial, considering the roots with multiplicities as independent roots.

The number of positive or negative real roots or zeros is either equal to the number of sign changes of f(x) or f(-x) or less than the number of sign changes by an even number.
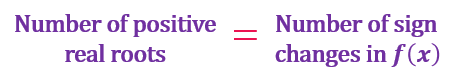
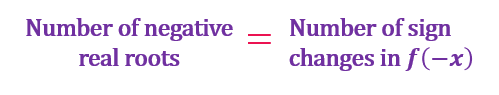
If the number of positive or negative real roots is 0 or 1, then the actual number of roots will be that itself, as an even number cannot further reduce it. Hence, 0 or 1 in any chart column is not to be altered throughout the chart. The roots that are not real are imaginary or complex, and the imaginary roots always occur in pairs. For example, if 1+ i is a root, then 1-i is also a root. The number of complex roots can be obtained by subtracting the sum of positive and real roots from the degree of the polynomial.
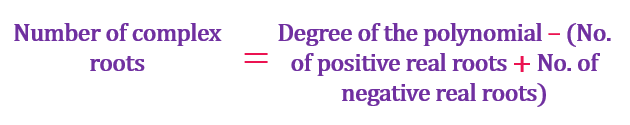
Considering the same example, f(x)=ax6-bx5+cx4-dx3+ex2+gx+h
Here, the possible number of positive real roots is 4,2,0, and the possible number of negative real roots is 2,0. Hence, Descartes's rule of signs chart can be constructed as follows:

Conclusion
Descartes's rule of signs states that for any polynomial f(x) in standard form, without any zero coefficient terms, the number of positive real roots will be either equal to the number of sign changes of the coefficients or down by an even number. The number of negative real roots is either equal to the number of sign changes of the coefficients of f(-x) or down by an even number. The rule will not give the actual number of roots but the possible number of roots. If the number of sign changes of f(x) or f(-x) is 0 or 1, then that itself is the actual number of real roots as it cannot be decreased further by an even number anymore. The number of complex roots can be found using Descartes's sign rule chart.
Solved Examples
Q1. Find the number of positive real roots for the polynomial 3x2–x–12–x4+x3.
Ans: Here, f(x)= 3x2–x–12–x4+x3
f(x) is not in standard form. The standard form of a polynomial is expressed by arranging the terms in the descending order of powers of the variables. So, f(x) in standard form is
f(x)= –x4+x3+3x2–x–12
Now, observe the sign changes in f(x).
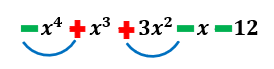
We can see that there are two sign changes; hence, the number of positive real roots can be either 2 or down by an even number, 2-2=0. It has 2 sign changes. Hence, 2 or 0 positive roots.
Q2. Find the possible number of real roots of the polynomial 2x3-x2-15 x+24.
Ans: Given polynomial is f(x)=2x3-x2-15x+24
We can see that there are two sign changes in the coefficients of f(x).
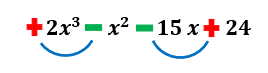
The number of possible positive real roots will be either equal to the number of sign changes or down by an even number. Hence, the possible positive roots are 2 or 0. Now, to find the possible number of negative real roots, let us first find out f(-x).
f(-x)=2(-x)3-(-x)2-15(-x)+24
⇒f(-x)=-2x3-x2+15x+24
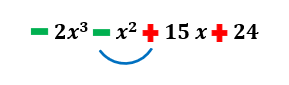
f(-x) has only 1 sign change. Hence, the possible number of negative roots will be 1.
Hence, 2x2-x2-15x+24 can have 2 positive real roots and 1 negative real root.
Q3. Find the possible number of combination of real and imaginary roots for the polynomial f(x) =x5 –3x3+6x2–28x+24.
Ans: Here, f(x) =x5 –3x3+6x2–28x+24

We can see that there are 4 sign changes. So, the possible number of positive real roots will be 4 or 4-2=2 or 2-2=0. The number of negative real roots is either at most the number of sign changes in the sequence of the polynomial coefficients of f(-x), eliminating the zero coefficients or down by an even number.
f(-x) =(-x)5 –3(-x)x3+6(-x)x2–28(-x)+24
⇒f(-x)=-x5 +3x3+6x2+28x+24
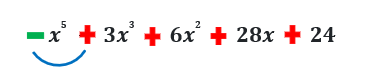
There is only 1 sign change in f(-x). Hence, the possible number of negative roots is one.
Since the degree of the given polynomial is 5, there will be 5 roots for f(x). The number of complex roots is obtained by subtracting the sum of positive and real roots from the degree of the polynomial.
So, Descartes's sign rule chart can be constructed as given below:
