The modulus function is a function that gives the magnitude of the number or variable or its combination. It is also called an absolute function. The output of this function will always be positive, no matter what the input was fed into the function. The modulus function can be plotted on a two-dimensional plane, and slight modifications in the argument of the functions can result in various shifts in the graphs.
The modulus function is defined as
Or it can also be stated as
is read as modulus or mod of .
Some examples of modulus function are
The modulus function can be plotted on a two-dimensional plane. Let us first see the graphs and .
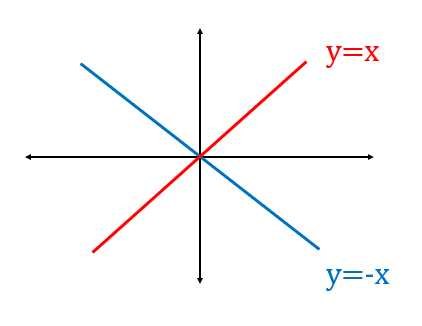
The function value cannot be negative when it comes to a modulus function. And hence, the values cannot be negative for any . So the graph of will be trimmed below the axis, and it will be as follows:
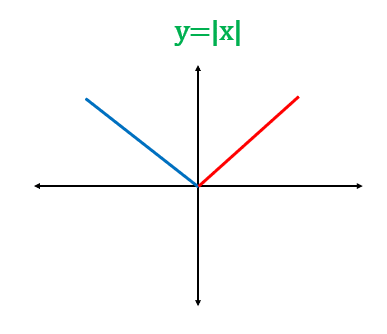
The graph of and will be the same.
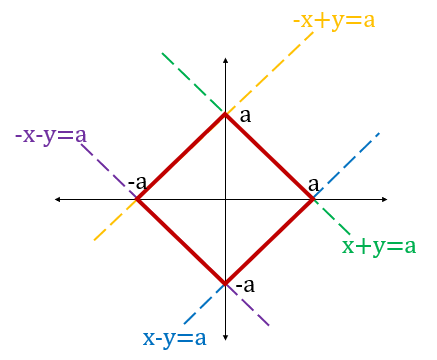
The expression is equivalent to the following four relations, along with the conditions on and .
if and are in the first quadrant
if and are in the fourth quadrant
if and , are in the second quadrant
if and are in the third quadrant
The four lines are plotted as dotted lines in the following graph. The graph of is the only part which satisfies all the above conditions. The bold line shows the graph of . Thus the graph of will be a square rotated at with a diagonal length of . The side will be .
The graph of is a V-shaped graph. Now, let us see how the graph will change when the arguments inside and outside the function are changing. The change in the arguments can shift the graph vertically and horizontally. The possible change in arguments of are
The function graph shifts upwards when a constant is added to the function, the constant being positive.
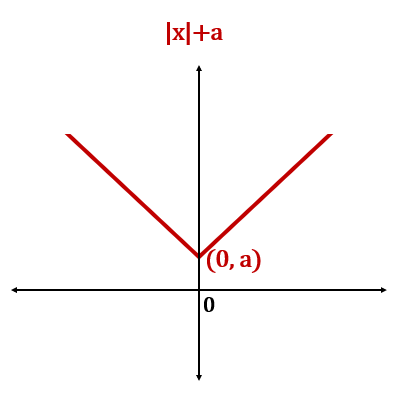
The function graph shifts downwards when a negative constant is added to the function.
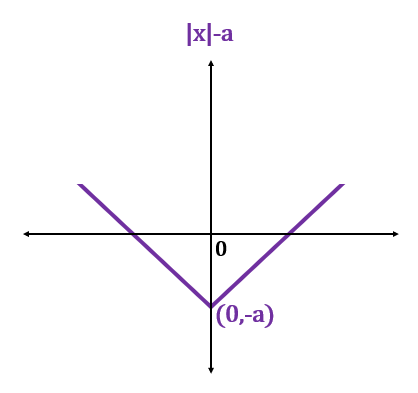
If a negative constant is added to the function argument, the function shifts right.
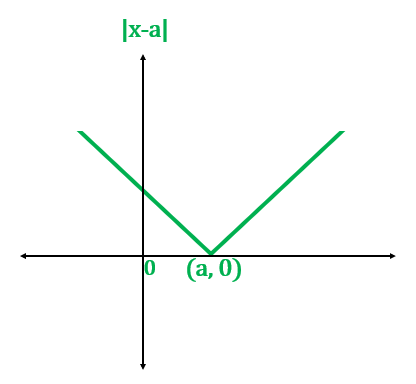
If a positive constant is added to the function argument, the function shifts to the left.
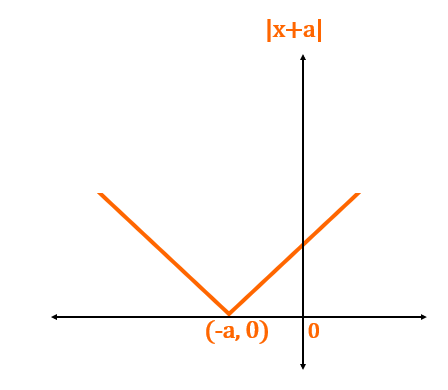
More shifts can be possible by combining the above conditions. Adding constants will enable the following shifts.
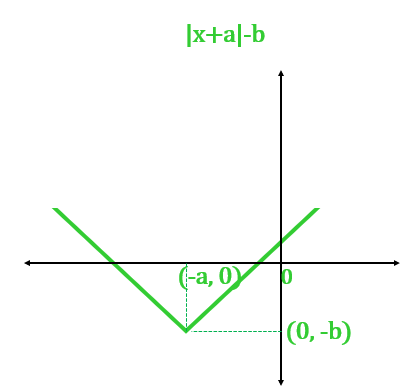
For , the function shifts down and right.
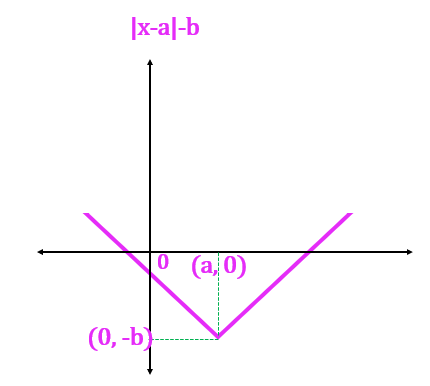
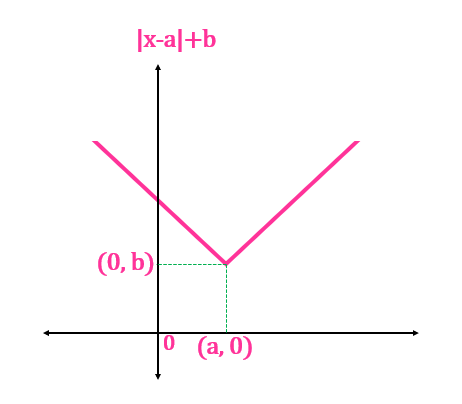
For , the function shifts up and right.
For , the function shifted down and left.
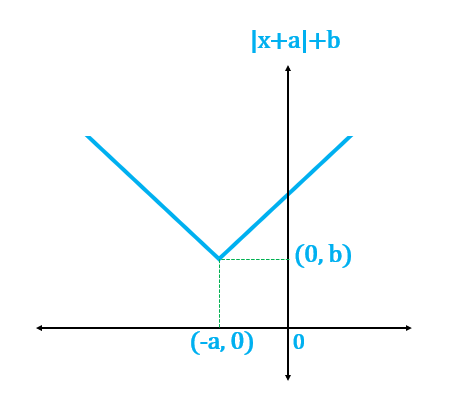
For , the function shifted up and left.
In short, we can say that,
The function shifts right when a negative constant is added to in
For example:
The function shifts left when a positive constant is added to in
For example:
The function shifts up and right when a positive constant is added to and a negative constant is added to in
For example:
The function shifts up and left when a positive constant is added to and a positive constant is added to in
For example:
The function shifts down and left when a negative constant is added to and a positive constant is added to in
For example:
The function shifts down and left when a negative constant is added to and a negative constant is added to in
For example:
Q1. Find the length of the diagonal of the square .
Ans: The graph of will be a square rotated at with a diagonal length of , and the side will be .
Here, .
So, the length of the diagonal of the square is units
Q2. What is the area enclosed by the graph of ?
Ans: The graph of will be a square rotated at with a diagonal length of , and the side will be .
So, for ,
So, the length of the square
The area of a square of side length a is .
Hence the area of the given square is sq. units
Q3. Find the number of integer solutions to
Ans: The graph of will be a square rotated at with a diagonal length of , and a side length .
So, the solutions of will lie on this square, so we can count them if we need integer solutions.
For , the maximum value can take is when .
We can see the possible solutions below:
When , there will be solutions
When , there will be solutions
When , there will be solutions
When , there will be solutions
When , there will be solutions
When , there will be solutions
Hence, there will be integral solutions
Modulus Function Definition
The modulus function is defined as
Or it can also be stated as
is read as modulus or mod of .
Some examples of modulus function are
Graph of a Modulus Function
The modulus function can be plotted on a two-dimensional plane. Let us first see the graphs and .

The function value cannot be negative when it comes to a modulus function. And hence, the values cannot be negative for any . So the graph of will be trimmed below the axis, and it will be as follows:
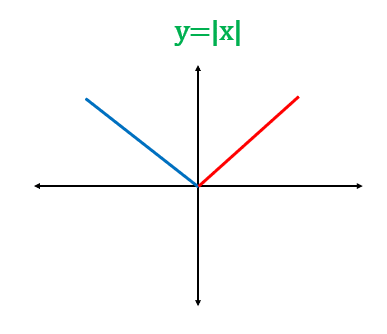
The graph of and will be the same.
Graph of |x|+|y|=a
The expression is equivalent to the following four relations, along with the conditions on and .
if and are in the first quadrant
if and are in the fourth quadrant
if and , are in the second quadrant
if and are in the third quadrant
The four lines are plotted as dotted lines in the following graph. The graph of is the only part which satisfies all the above conditions. The bold line shows the graph of . Thus the graph of will be a square rotated at with a diagonal length of . The side will be .

Shifts in Graph Positions
The graph of is a V-shaped graph. Now, let us see how the graph will change when the arguments inside and outside the function are changing. The change in the arguments can shift the graph vertically and horizontally. The possible change in arguments of are
The function graph shifts upwards when a constant is added to the function, the constant being positive.

The function graph shifts downwards when a negative constant is added to the function.

If a negative constant is added to the function argument, the function shifts right.

If a positive constant is added to the function argument, the function shifts to the left.

More shifts can be possible by combining the above conditions. Adding constants will enable the following shifts.
For , the function shifts down and right.

For , the function shifts up and right.

For , the function shifted down and left.

For , the function shifted up and left.

In short, we can say that,
- The function shifts up when a positive constant is added to
- The function shifts down when a negative constant is added to
The function shifts right when a negative constant is added to in
For example:
The function shifts left when a positive constant is added to in
For example:
The function shifts up and right when a positive constant is added to and a negative constant is added to in
For example:
The function shifts up and left when a positive constant is added to and a positive constant is added to in
For example:
The function shifts down and left when a negative constant is added to and a positive constant is added to in
For example:
The function shifts down and left when a negative constant is added to and a negative constant is added to in
For example:
Solved Examples
Q1. Find the length of the diagonal of the square .
Ans: The graph of will be a square rotated at with a diagonal length of , and the side will be .
Here, .
So, the length of the diagonal of the square is units
Q2. What is the area enclosed by the graph of ?
Ans: The graph of will be a square rotated at with a diagonal length of , and the side will be .
So, for ,
So, the length of the square
The area of a square of side length a is .
Hence the area of the given square is sq. units
Q3. Find the number of integer solutions to
Ans: The graph of will be a square rotated at with a diagonal length of , and a side length .
So, the solutions of will lie on this square, so we can count them if we need integer solutions.
For , the maximum value can take is when .
We can see the possible solutions below:
When , there will be solutions
When , there will be solutions
When , there will be solutions
When , there will be solutions
When , there will be solutions
When , there will be solutions
Hence, there will be integral solutions