Polynomials are algebraic expressions with whole number powers. A polynomial can be expressed in the general form, and its roots of it can be determined. The coefficients of the polynomials give many hints about the characteristics of the roots of the equations.
An algebraic expression is an expression which is made up of variables and constants along with basic mathematical operations of addition, subtraction, multiplication and division. An algebraic expression can be of a single term, two, three, or more than three terms. An algebraic expression of a single term is called a monomial, with two terms is called a binomial and with three terms is called a trinomial.
Examples of algebraic expressions are ....
The degree of an algebraic expression is the highest power of variables in a term in an expression.
Based on the degree, algebraic expressions are classified as linear, quadratic, and cubic expressions with degrees and , respectively. Polynomials are algebraic expressions with the degree of the expression as whole numbers. All polynomials are algebraic expressions, but all algebraic expressions need not be polynomials. The standard form of a polynomial is
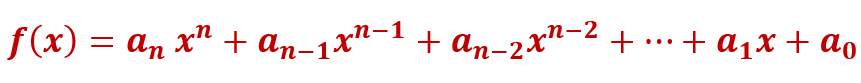
Where are rational numbers and . This is the standard form of a general equation of degree.
Roots of the General Equation or Polynomial
The roots of a polynomial are the value of the variable for which the polynomial equation equals zero. For a degree equation, there will be at most roots. That means, for a linear equation, there will be only root. For a quadratic, there will be ; for cubic, there will be roots.
For example,
If is the root of a polynomial equation , then the polynomial is exactly divisible by , or we can say that is the factor of the given polynomial .
Let the roots of the polynomial .
Then the sum of the roots
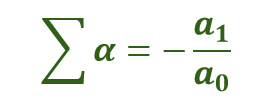
The sum of the product of roots taken two at a time
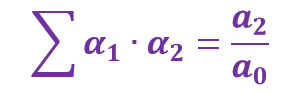
The sum of the product of roots taken three at a time
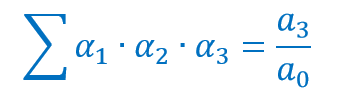
The product of roots
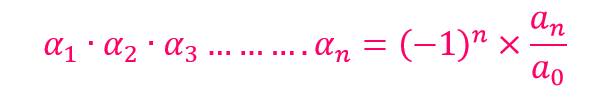
The roots of a polynomial may be real or imaginary. When imaginary or complex roots are present, they occur in conjugate pairs. That is, if is a root, then will also be a root.
Similarly, if the roots of the equation are surds, then they also occur in conjugate pairs. That is, is a root, then is also a root.
If is the rational root of the equation , then divides and divides .
An equation's coefficients can hint at the nature of the roots.
Solved Examples
Q1. Find the number of real roots of the equation .
Ans:
We know that if the equation contains only even powers of and the coefficients are all of the same sign, the equation has no real root. Hence, the given equation has no real root.
Q2. If the roots of the equation are in arithmetic progression, find the value of .
Ans: As the roots are in arithmetic progression, let the roots of the given equation be .
Then, the sum of the roots
Sum of the roots
Since is a root, it satisfies the polynomial.
So,
Q3. Find the roots of equation , given that its roots are in geometric progression.
Ans: Let the roots of the given equation be
Then, the product of the roots
Products of the root
Since is a root, is a factor.
Dividing the given polynomial by the factor, we get the other factor as .
The roots of this factor can be found using the quadratic formula as
Therefore, the roots of the given equation are .
Polynomials
An algebraic expression is an expression which is made up of variables and constants along with basic mathematical operations of addition, subtraction, multiplication and division. An algebraic expression can be of a single term, two, three, or more than three terms. An algebraic expression of a single term is called a monomial, with two terms is called a binomial and with three terms is called a trinomial.
Examples of algebraic expressions are ....
The degree of an algebraic expression is the highest power of variables in a term in an expression.
- For example, the degree of is .
- The degree of is as the power of is and is , and so the power of the expression will be
- The degree of is .
- The degree of is as the degree of is .
Based on the degree, algebraic expressions are classified as linear, quadratic, and cubic expressions with degrees and , respectively. Polynomials are algebraic expressions with the degree of the expression as whole numbers. All polynomials are algebraic expressions, but all algebraic expressions need not be polynomials. The standard form of a polynomial is
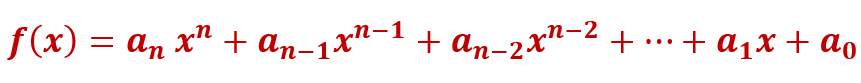
Where are rational numbers and . This is the standard form of a general equation of degree.
Roots of the General Equation or Polynomial
The roots of a polynomial are the value of the variable for which the polynomial equation equals zero. For a degree equation, there will be at most roots. That means, for a linear equation, there will be only root. For a quadratic, there will be ; for cubic, there will be roots.
For example,
- has just one root.
- has at most roots.
- can have at most roots.
If is the root of a polynomial equation , then the polynomial is exactly divisible by , or we can say that is the factor of the given polynomial .
Let the roots of the polynomial .
Then the sum of the roots
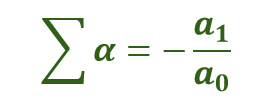
The sum of the product of roots taken two at a time
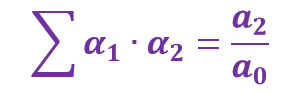
The sum of the product of roots taken three at a time
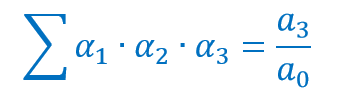
The product of roots
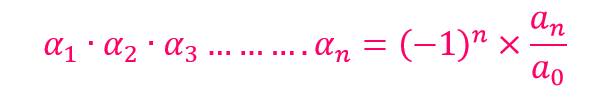
The roots of a polynomial may be real or imaginary. When imaginary or complex roots are present, they occur in conjugate pairs. That is, if is a root, then will also be a root.
Similarly, if the roots of the equation are surds, then they also occur in conjugate pairs. That is, is a root, then is also a root.
If is the rational root of the equation , then divides and divides .
An equation's coefficients can hint at the nature of the roots.
- If the coefficients of an equation are all positive, then the equation has no positive root.
- If, in the equation, the coefficients of even powers of are all of one sign, and the coefficients of the odd powers are all of opposite sign, then the equation has no negative root.
- If the equation contains only even powers of and the coefficients are all of the same sign, the equation has no real root.
- If the equation contains only odd powers of , and the coefficients are all of the same sign, the equation has no real roots except .
- Descartes's rule of signs
- An equation in standard form with non-zero coefficients cannot have more positive roots than the number of sign changes of the coefficients of .
- The equation cannot have more negative roots than the number of sign changes of the coefficients of
Solved Examples
Q1. Find the number of real roots of the equation .
Ans:
We know that if the equation contains only even powers of and the coefficients are all of the same sign, the equation has no real root. Hence, the given equation has no real root.
Q2. If the roots of the equation are in arithmetic progression, find the value of .
Ans: As the roots are in arithmetic progression, let the roots of the given equation be .
Then, the sum of the roots
Sum of the roots
Since is a root, it satisfies the polynomial.
So,
Q3. Find the roots of equation , given that its roots are in geometric progression.
Ans: Let the roots of the given equation be
Then, the product of the roots
Products of the root
Since is a root, is a factor.
Dividing the given polynomial by the factor, we get the other factor as .
The roots of this factor can be found using the quadratic formula as
Therefore, the roots of the given equation are .