Polygons: Polygons are simple, closed figures made up of only line segments. It is a flat or plane, two-dimensional closed shape bounded with straight sides. It cannot have curved sides. The sides of a polygon are called its edges. The points where two sides meet are a polygon's vertices (or corners). The smallest polygon will have 3 sides, and the number of sides can increase to any integral value.
Polygons are classified into convex and concave based on the interior angles of a polygon. If the measure of all the interior angles of a polygon are less than 180 degrees, then it is a convex polygon. It is a concave polygon if any interior angle is greater than 180 degrees.

Polygons are also classified as regular and irregular polygons based on the measures of their sides and angles. If the sides of a polygon are equal in length and all angles are equal in measure, then it is a regular polygon. Otherwise, it is an irregular polygon. An equilateral triangle is a 3-sided regular polygon with all equal sides and angles equal to 60°. A square is a regular quadrilateral with equal sides and angles equal to 90°.
Every polygon will have two types of angles: Interior angles and Exterior angles
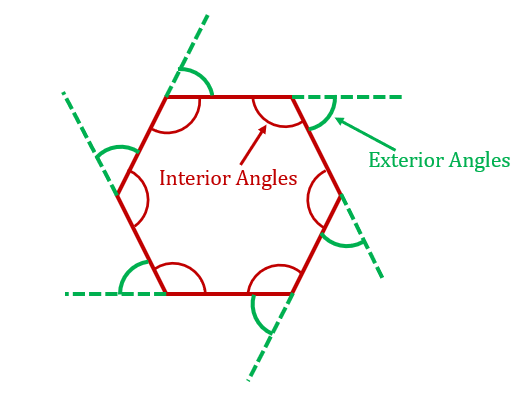
The interior angles are formed between the adjacent sides inside the polygon. They are equal to each other in the case of a regular polygon. The number of interior angles in a polygon is equal to the number of sides. An exterior angle of the polygon is formed by extending one side of the polygon either in the clockwise or anticlockwise direction. Then, the angle between that extension and the adjacent side is measured to get the exterior angle. The measure of all the exterior angles of a regular polygon are equal. Sum of Interior Angles of a Polygon For a polygon of n sides, the sum of the interior angles of a polygon can be found by using the formula:
For example, for a regular hexagon, n=6. Sum of interior angles of the hexagon =(6-2)×180°=4×180°=720°
For any regular polygon,
Measure of Each Interior Angle of a Regular Polygon =((n-2)180°)/n
So, the measure of an interior angle of a regular hexagon will be (720°)/6=120°
For any polygon of n sides, the sum of all the exterior angles is equal to a complete angle.
The measure of an exterior angle of a regular polygon is obtained by dividing the sum of angles by the number of sides. The measure of each exterior angle =(360°)/n
Q1. Find the sum of angles of the interior angles of a dodecagon.
Ans: The sum of the interior angles of a polygon =(n-2)180° Dodecagon has 12 sides and so n=12 Hence, the sum of all the interior angles of a dodecagon =(12-2)×180°=1800°
Q2. Can a regular polygon have the sum of interior angles equal to 1440°?
Ans: The sum of the interior angles of a polygon =(n-2)180° We need to find whether there is a n for which (n-2)180°= 1440° (n-2)180°= 1440° ⇒(n-2)=(1440°)/(180°) ⇒(n-2)=8 ⇒n=8+2=10 Hence, a decagon of 10 sides has the sum of interior angles equal to 1440°.
Q3. What will be the measure of each exterior angle of a regular nonagon?
Ans: A regular nonagon is a polygon with 9 equal sides. The sum of all the exterior angles of a polygon is 360°, and the measure of an exterior angle of a regular polygon is (360°)/n. Thus, the measure of an exterior angle of a nonagon =(360°)/9=40°
Polygons Definition
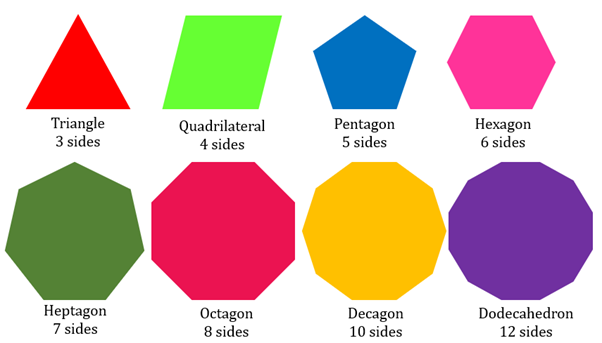
A polygon is a simple, closed, two-dimensional figure formed by only straight lines. The smallest polygon is a triangle, made up of three line segments. The four-sided polygon is a quadrilateral, and a 5 sided polygon is named a pentagon. Six line segments are joined to form a hexagon, 7 line segments form a heptagon, 8 line segments form an octagon, 9 line segments form a nonagon and 10 line segments form a decagon. Polygons with more number of sides also have names like a dodecagon, that has 12 sides and an icosagon, which has 20 sides.
Types of Polygons
Polygons are classified into convex and concave based on the interior angles of a polygon. If the measure of all the interior angles of a polygon are less than 180 degrees, then it is a convex polygon. It is a concave polygon if any interior angle is greater than 180 degrees.

Polygons are also classified as regular and irregular polygons based on the measures of their sides and angles. If the sides of a polygon are equal in length and all angles are equal in measure, then it is a regular polygon. Otherwise, it is an irregular polygon. An equilateral triangle is a 3-sided regular polygon with all equal sides and angles equal to 60°. A square is a regular quadrilateral with equal sides and angles equal to 90°.
Angles of a Polygon
Every polygon will have two types of angles: Interior angles and Exterior angles

The interior angles are formed between the adjacent sides inside the polygon. They are equal to each other in the case of a regular polygon. The number of interior angles in a polygon is equal to the number of sides. An exterior angle of the polygon is formed by extending one side of the polygon either in the clockwise or anticlockwise direction. Then, the angle between that extension and the adjacent side is measured to get the exterior angle. The measure of all the exterior angles of a regular polygon are equal. Sum of Interior Angles of a Polygon For a polygon of n sides, the sum of the interior angles of a polygon can be found by using the formula:
Sum of Interior Angles of a Polygon=(n-2)180°
For example, for a regular hexagon, n=6. Sum of interior angles of the hexagon =(6-2)×180°=4×180°=720°
For any regular polygon,
Measure of Each Interior Angle of a Regular Polygon =((n-2)180°)/n
So, the measure of an interior angle of a regular hexagon will be (720°)/6=120° Sum of Exterior Angles of a Polygon
For any polygon of n sides, the sum of all the exterior angles is equal to a complete angle.
Sum of Exterior Angles of a Polygon =360°
The measure of an exterior angle of a regular polygon is obtained by dividing the sum of angles by the number of sides. The measure of each exterior angle =(360°)/n
Solved Examples
Q1. Find the sum of angles of the interior angles of a dodecagon.
Ans: The sum of the interior angles of a polygon =(n-2)180° Dodecagon has 12 sides and so n=12 Hence, the sum of all the interior angles of a dodecagon =(12-2)×180°=1800°
Q2. Can a regular polygon have the sum of interior angles equal to 1440°?
Ans: The sum of the interior angles of a polygon =(n-2)180° We need to find whether there is a n for which (n-2)180°= 1440° (n-2)180°= 1440° ⇒(n-2)=(1440°)/(180°) ⇒(n-2)=8 ⇒n=8+2=10 Hence, a decagon of 10 sides has the sum of interior angles equal to 1440°.
Q3. What will be the measure of each exterior angle of a regular nonagon?
Ans: A regular nonagon is a polygon with 9 equal sides. The sum of all the exterior angles of a polygon is 360°, and the measure of an exterior angle of a regular polygon is (360°)/n. Thus, the measure of an exterior angle of a nonagon =(360°)/9=40°