An equation is a statement connecting two expressions by an equality sign. A polynomial is an algebraic expression whose variable powers are whole numbers. A quadratic equation is a second-order polynomial equation in one variable in the form of , where are real number constants and .
A second-order polynomial equation in one variable in the form where are real number constants and is called a quadratic equation. The standard form of a quadratic equation is
For example,
The quadratic expressions can be of three types: ax^2+c,ax^2+bx,ax^2+bx+c.
As the degree of a quadratic equation is , there will be at most roots for a quadratic equation. The roots of the equation can be found using various methods like
We can factorise the polynomial in the form . and are the roots of the equation.
An expression of the form is a perfect square. We can convert a given quadratic equation into a perfect square as below:
The value of can be found using the quadratic formula as
Here, and
All quadratic functions can be plotted on a two-dimensional plane by finding their value for .
Since quadratic is a second-order function, the shape of the graph will be a parabola.
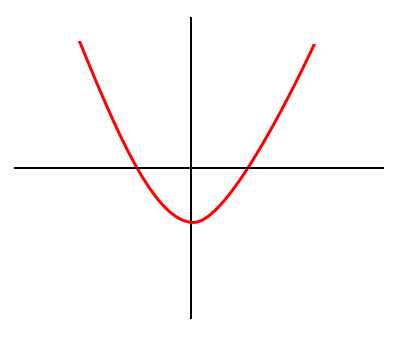
For a quadratic equation in the form , the opening of the curve will be dependent on the leading coefficient, that is, the coefficient of .
If , then the curve will open upwards
If , then the curve will open downwards
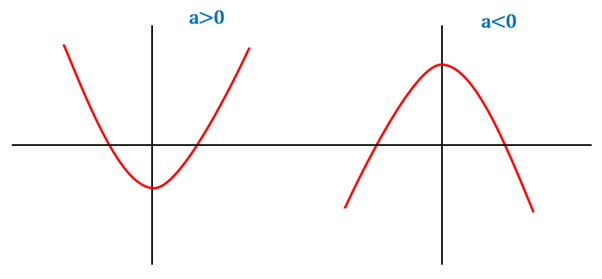
A quadratic function's maximum and minimum value will be at the vertex of the graph. The points are shown below:
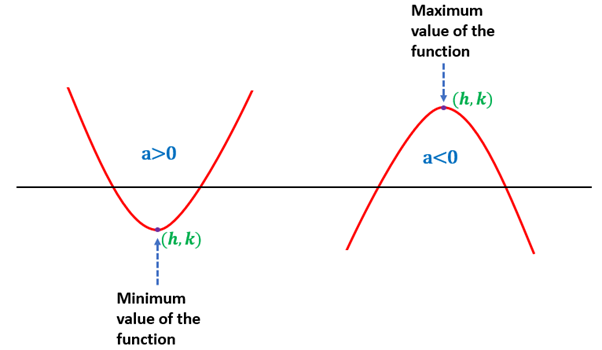
If , then the function will have a minimum point. If , then the function will have a maximum point. The coordinate of the vertex of the graph can be found as
can be found by substituting for in .
The maximum and minimum values of a quadratic equation can be found by completing the square method.
Case 1:
As is either positive or , the minimum value of occurs when is . Hence, the minimum value of the function is .
Case 2:
As is either negative or , the maximum value of occurs when is . Hence, the maximum value of the function is .
The nature of the roots of a quadratic equation can be identified before finding the roots. We can check that by observing the discriminant.
For a quadratic equation in standard form
The discriminant
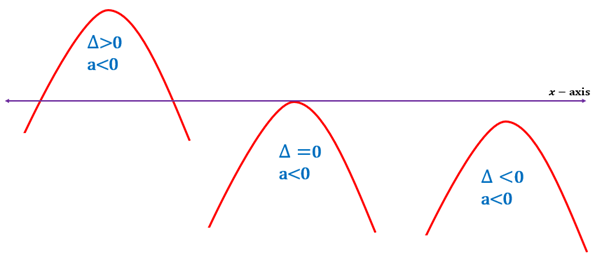
The points where the graph touches the axis depend on the values of .
If the is real, the graph touches at most two points on axis.
If is , then the graph touches the axis at only one point.
If is imaginary, then the graph will not touch axis at any points.
When , all the graphs will open upwards for the three conditions of the discriminant.
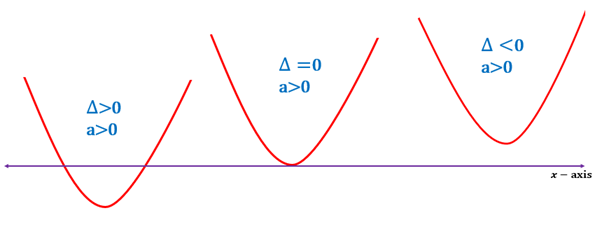
When , all the graphs will open upwards for the three conditions of the discriminant.
If , the value of is
The minimum value of the expression occurs at
If , the value of is
The maximum value of the expression occurs at
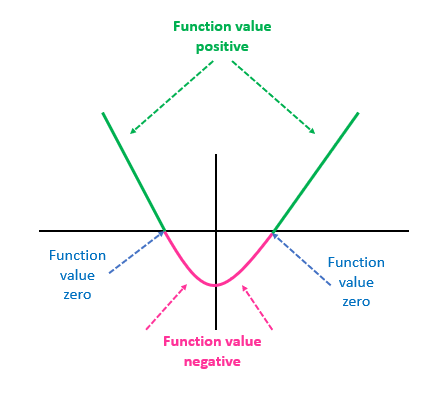
The expression always have the same sign as , except when lies between and , where and area real values of intercepts on the axis. If and are the roots of the quadratic equation, then the value of the quadratic expression changes sign only when the curve crosses the axis. As the curve crosses the axis at the point where its value becomes zero, the curve changes sign at , where .
The coefficients of the quadratic equation can hint at the roots of the equation. For the equation ,
We can factorise the polynomial in the form .
Then, if
⇒ The sum of the roots of the quadratic equation,
And the product of the roots of the quadratic equation
Q1. Find the number of real roots of the equation .
Ans: To find the nature of the roots, we need to find the discriminant of the function.
Discriminant
Here, and
Since the discriminant is less than , the two roots will be imaginary; hence, there will be no real roots for the given function.
Q2. Find the roots of the equation using the quadratic formula.
Ans: The roots of the quadratic equation can be found by the quadratic method as
Here,
Hence, the roots are and
Q3. For a quadratic equation of , will there be a maximum or minimum value? Find the value.
Ans: We can see that the leading coefficient , and so the graph of the function will be opening upwards and hence the function will have a minimum value.
We can factorise the given quadratic equation as
Now the function is in the form
The minimum value of the expression occurs at
The coordinate can be found by substituting instead of in the equation, and we get
Hence, the minimum value of the function occurs at .
Quadratic Equation Definition
A second-order polynomial equation in one variable in the form where are real number constants and is called a quadratic equation. The standard form of a quadratic equation is
For example,
The quadratic expressions can be of three types: ax^2+c,ax^2+bx,ax^2+bx+c.
Roots of a Quadratic Equation
As the degree of a quadratic equation is , there will be at most roots for a quadratic equation. The roots of the equation can be found using various methods like
- Factorisation
We can factorise the polynomial in the form . and are the roots of the equation.
- Completing the square method
An expression of the form is a perfect square. We can convert a given quadratic equation into a perfect square as below:
- Quadratic formula
The value of can be found using the quadratic formula as
Here, and
Graph of a Quadratic Equation
All quadratic functions can be plotted on a two-dimensional plane by finding their value for .
Since quadratic is a second-order function, the shape of the graph will be a parabola.

For a quadratic equation in the form , the opening of the curve will be dependent on the leading coefficient, that is, the coefficient of .
If , then the curve will open upwards
If , then the curve will open downwards

Minimum and Maximum Value of a Quadratic Function
A quadratic function's maximum and minimum value will be at the vertex of the graph. The points are shown below:

If , then the function will have a minimum point. If , then the function will have a maximum point. The coordinate of the vertex of the graph can be found as
can be found by substituting for in .
The maximum and minimum values of a quadratic equation can be found by completing the square method.
Case 1:
As is either positive or , the minimum value of occurs when is . Hence, the minimum value of the function is .
Case 2:
As is either negative or , the maximum value of occurs when is . Hence, the maximum value of the function is .
Nature of Roots of Quadratic Equation
The nature of the roots of a quadratic equation can be identified before finding the roots. We can check that by observing the discriminant.
For a quadratic equation in standard form
The discriminant
- If , then the function has two real distinct roots
- If , then the function has two real equal roots
- If , then the function has two imaginary roots
- If is a perfect square, then the roots will be rational and unequal.
The points where the graph touches the axis depend on the values of .
If the is real, the graph touches at most two points on axis.
If is , then the graph touches the axis at only one point.
If is imaginary, then the graph will not touch axis at any points.
When , all the graphs will open upwards for the three conditions of the discriminant.

When , all the graphs will open upwards for the three conditions of the discriminant.

If , the value of is
- , when or
- Negative, when x lies between α and β
- Positive otherwise
The minimum value of the expression occurs at
If , the value of is
- , when or
- Positive, when x lies between α and β
- Negative otherwise
The maximum value of the expression occurs at
The expression always have the same sign as , except when lies between and , where and area real values of intercepts on the axis. If and are the roots of the quadratic equation, then the value of the quadratic expression changes sign only when the curve crosses the axis. As the curve crosses the axis at the point where its value becomes zero, the curve changes sign at , where .

The coefficients of the quadratic equation can hint at the roots of the equation. For the equation ,
- If , the roots are equal in magnitude but opposite in sign
- If , the roots are reciprocals of each other
- If and have the same sign, but b has the opposite sign, the roots are positive
- If and have the same sign, but c has the opposite sign, the roots have opposite signs.
Sum and Products of the Roots of the Quadratic Equation
We can factorise the polynomial in the form .
Then, if
⇒ The sum of the roots of the quadratic equation,
And the product of the roots of the quadratic equation
Solved Examples
Q1. Find the number of real roots of the equation .
Ans: To find the nature of the roots, we need to find the discriminant of the function.
Discriminant
Here, and
Since the discriminant is less than , the two roots will be imaginary; hence, there will be no real roots for the given function.
Q2. Find the roots of the equation using the quadratic formula.
Ans: The roots of the quadratic equation can be found by the quadratic method as
Here,
Hence, the roots are and
Q3. For a quadratic equation of , will there be a maximum or minimum value? Find the value.
Ans: We can see that the leading coefficient , and so the graph of the function will be opening upwards and hence the function will have a minimum value.
We can factorise the given quadratic equation as
Now the function is in the form
The minimum value of the expression occurs at
The coordinate can be found by substituting instead of in the equation, and we get
Hence, the minimum value of the function occurs at .