A polygon is a simple or complex closed figure that has a finite number of sides connected end-to-end by line segments. A star is a polygon made up of several line segments connected end to end with each other, known as its sides or edges.

Star polygons are non-convex, self-intersecting, Equilateral and Equiangular polygons. Non-convex means that you can draw a line between two points inside the star-shaped polygon that passes outside its perimeter. And also, at least one interior angle will be more than 180°. Self-intersecting means that we can build all the different star shapes starting from a regular polygon and prolonging its vertices until the extensions cross each other. Equilateral signifies that all the outer sides of the star-shaped polygon have the same length. Equiangular means that all the angles are of equal measure. Equilateral and equiangular automatically qualify star polygons as regular polygons.
Thomas Bradwardine and Johannes Kepler were the first to extensively study the geometry of regular star polygons. According to Kepler, a star polygon is a regular polygon that has been augmented by extending each side until it intersects a non-adjacent side, creating a vertex.
Construction of a Star Polygon
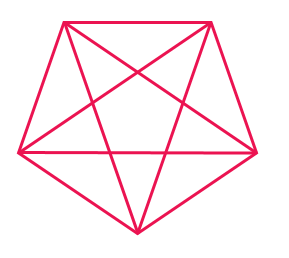
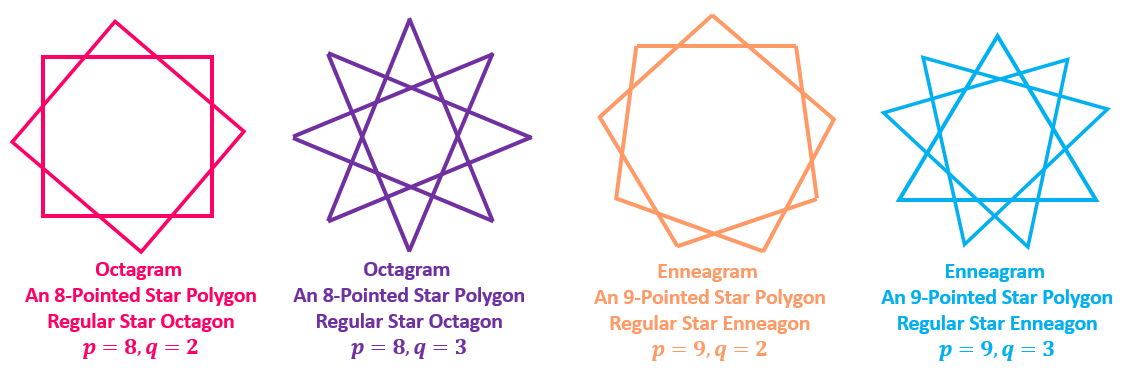
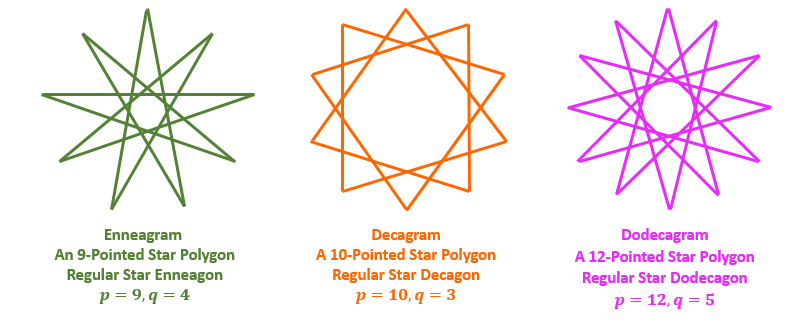
A regular star polygon is constructed by joining non-consecutive vertices of the regular convex polygons of continuous form. They are denoted by p/q , where p is the number of vertices of the convex regular polygon and q is the jump between vertices. Here, p/q must be an irreducible fraction, that is in simplest form. The polygon p/q is the same as the p/(p - q) , if the polygon is obtained by joining vertices in a counterclockwise direction.
More precisely, regular star polygons can be created by connecting one vertex of a simple, regular, p-sided polygon to another non-adjacent vertex and continuing the process until the original vertex is reached again. That is, considering two integers p and q, a star polygon is constructed by connecting every q^th point out of p points, regularly spaced in a circular placement.
q is the jump made between the connection of two vertices.
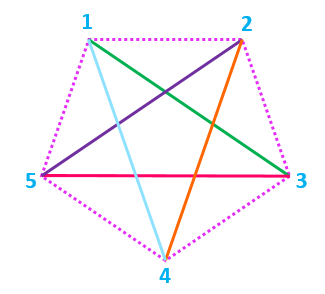
For instance, in a regular pentagon, a 5-pointed star can be obtained by drawing a line
from the 1st vertex to the 3rd vertex,
from the 3rd vertex to the 5th vertex,
from the 5th vertex to the 2nd vertex,
from the 2nd vertex to the 4th vertex, and
from the 4th vertex back to the 1st vertex.
In this example, p = 5 (5 vertices) and q = 2
q=2 because every second vertex is adjoined. Vertex 1 is connected to 3, and 3 is then connected to 5. 2 is connected to 4 and 4 is connected back to 1 after a jump of 2 when considering the vertices in circular order.
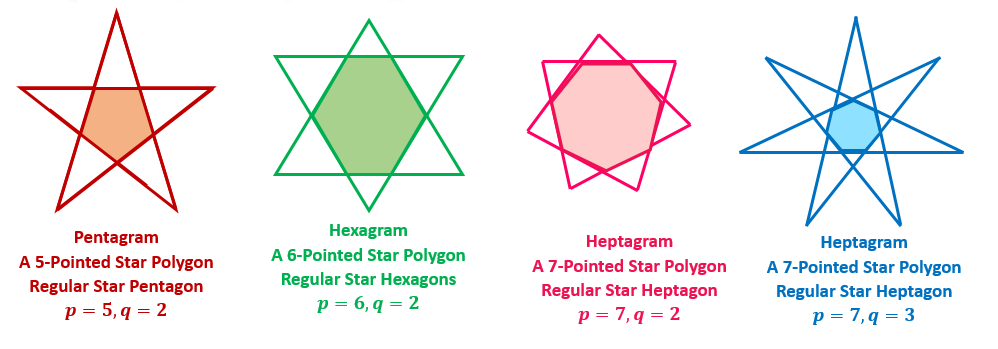
Types of Star Shapes
Sum of the Corner Angles in a n Pointed Star
Finding the sum of the corner or interior angles of a star polygon is a very tricky or confusing question. But, when the concept is understood, it is very easy to solve. There are two methods to find the corner angles.
- General method by visualizing polygons in the star
- Shortcut method
General Method to Find the Sum of the Interior Angles of a Star Polygon
Let us understand the general method through an example.
In the star diagram, find the sum of ∠A+∠B+∠C+∠D+∠E.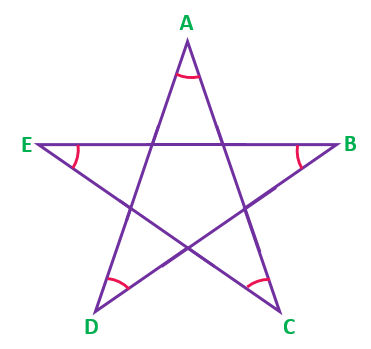
Solution: Mark points at the intersections and try to visualize triangles in the star. 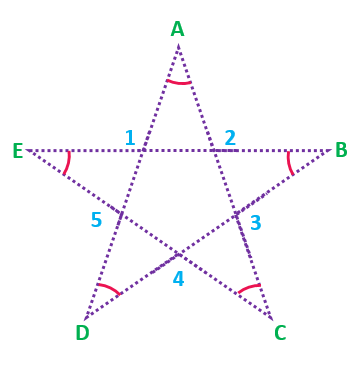
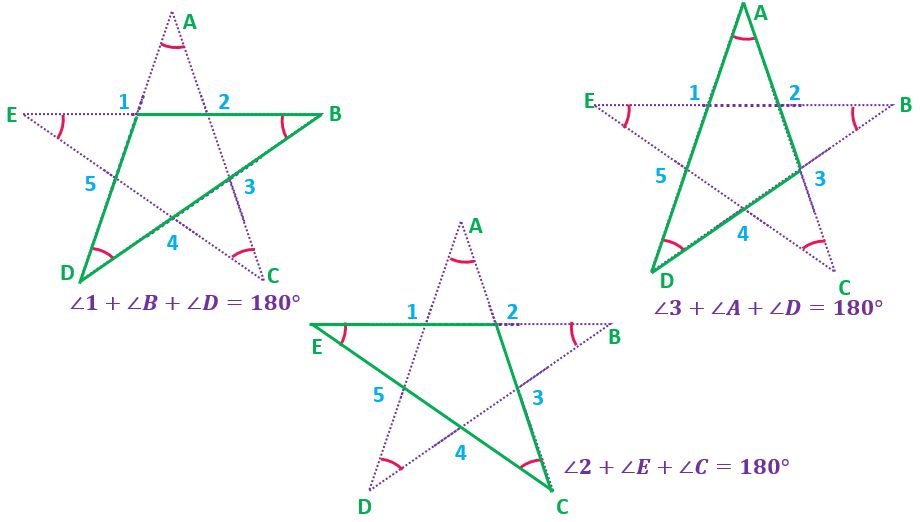
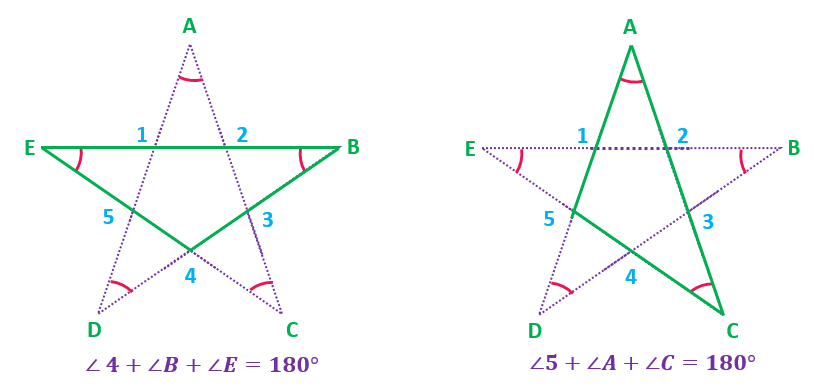
So, we will get
∠1+∠B+∠D=180°
∠2+∠E+∠C=180°
∠3+∠A+∠D=180°
∠4+∠B+∠E=180°
∠5+∠A+∠C=180°
Adding all these, we get
∠1+∠B+∠D+∠2+∠E+∠C+∠3+∠A+∠D+∠4+∠B+∠E+∠5+∠A+∠C=180°+180°+180°+180°+180°
⇒∠1+∠2+∠3+∠4+∠5+2(∠A+∠B+∠C+∠D+∠E)=5×180°
We can see that points 1,2,3,4,and 5 join to form a pentagon, and the sum of the interior angles of a pentagon is (5-2)180°=3×180°
⇒3×180°+2(∠A+∠B+∠C+∠D+∠E)=5×180°
⇒2(∠A+∠B+∠C+∠D+∠E)=5×180°-3×180°
⇒2(∠A+∠B+∠C+∠D+∠E)=2×180°
∠A+∠B+∠C+∠D+∠E=180°
Hence, the sum of the interior angles of the given star polygon is 180°. This method can be used to find the measure of angles of any polygon.
Shortcut Method to Find the Sum of the Interior Angles of a Star Polygon
In this method, we use a direct formula to calculate the sum of the interior angles of any star polygon.
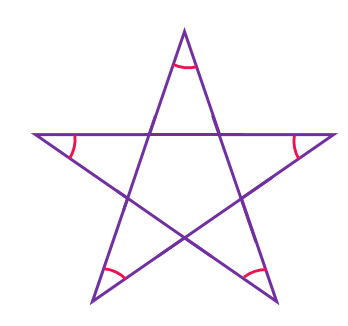
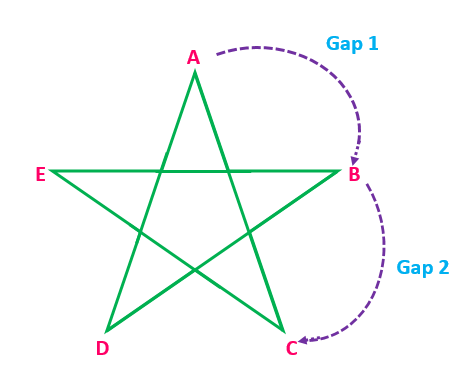
Sum of all angles =(n-2×gaps)×180° Here, gaps mean the number of jumps from one vertex to the vertex at the opposite end. Considering the previous example, we have n=5, and there are 2 gaps between two vertices.
So, Sum of all angles =∠A+∠B+∠C+∠D+∠E=(5-2×2)180°=(5-4)180°=180°
Solved Examples
Qn1. Find the sum of the angles at the points of the enneagram ABCDEFGHI.
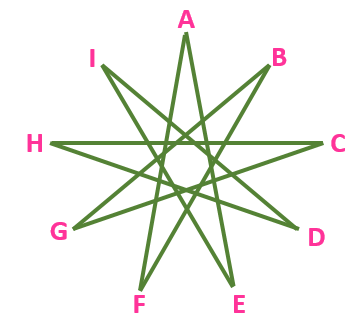
Solution: We know that an enneagram is a 9-pointed star. We also know that in any star polygon, Sum of all angles =(n-2×gaps)×180° We can see in the figure that A is connected to E. That is, there are 4 jumps between each connection of vertices. So, here, we have n=9, and gaps=4 Sum of all angles =∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I =(9-4×2)180° =(9-8)×180° =1×180°=180°
Qn2. Find the sum of the angles at the points of the 10-pointed star ABCDEFGHIJ.
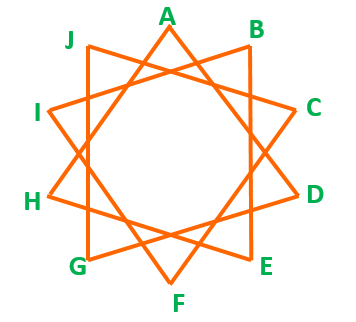
Solution: We know that in any star polygon, Sum of all angles =(n-2×gaps)×180° We can see in the figure that A is connected to D. That is, there are 3 jumps between each connection of vertices. So, here, we have n=10, and gaps=3 Sum of all angles =∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J =(10-3×2)180° =(10-6)×180° =4×180°=720°